Recent Posts
Recent Comments
게으른개발너D
[JS] 백트래킹 (Backtracking) 본문

✨ 백트래킹
- 모든 경우의 수를 탐색하는 알고리즘
- DFS나 BFS를 이용할 수 있다.
- 효율을 위해 탐색하지 않아도 되는 곳을 미리 막는 것을 가지치기 (Pruning)이라고 한다.
- 자바스크립트는 재귀 효율이 나쁘기 때문에 DFS를 구현할 경우 스택을 이용하는 것이 좋다.
- 코딩 테스트에선 이를 고려하여 재귀로 작성해도 풀 수 있도록 문제를 제출하는 경우도 있다.
- 탐색해서 순환 (Cycle)이 발생할 수 있다면 BFS를 이용하는 것이 편하다.
BFS, DFS
모든 경우의 수를 찾을 때도 사용한다.

백트래킹의 핵심은 가지치기!
가지치기를 얼마나 잘하느냐가 효율성을 결정한다.
✨ 백트래킹 로직 작성하는 방법
- 모든 경우의 수를 찾을 수 있도록 코딩
- 이후 문제에서 특정한 조건을 만족하는 것만 탐색하고 나머지는 탐색하지 않도록 조건물을 작성한다.
- 즉, 절대로 답이 될 수 없는 것은 탐색을 종료한다.
문제 예시 ) N-Queen
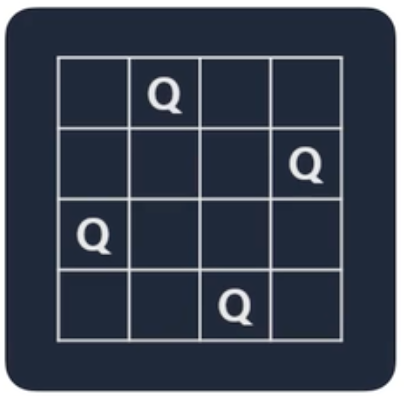
길이가 N인 체스판 위에 N개의 퀸이 서로를 공격할 수 없도록 배치할 수 있는 경우의 수는?
백트래킹은 모든 경우의 수를 찾아야 하기에 일단 하고본다!ㅋㅋㅋ
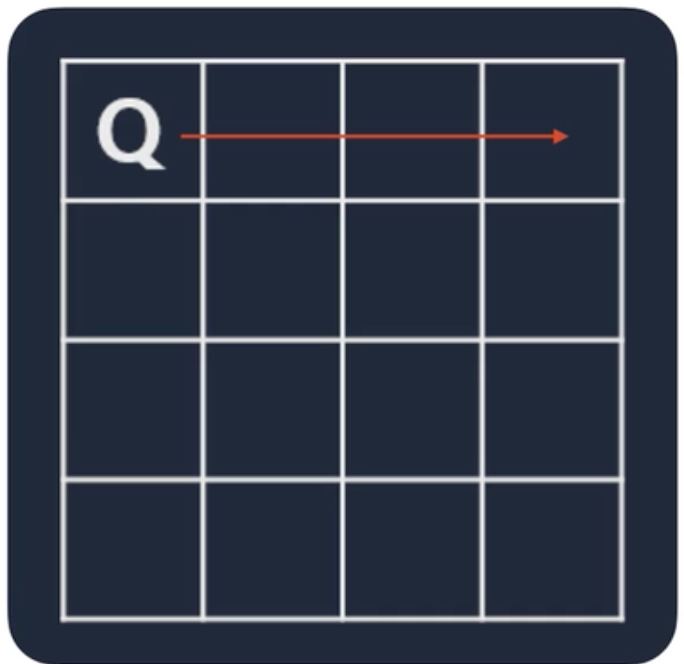
| 일단 뭔가를 해야하기 때문에 먼저 (1, 1)에 퀸을 배치한다. |  |
| 여기서 가지치기를 할 수 있다. 첫 줄은 더 이상 퀸을 둘 수 없기 때문에 바로 다음 줄로 이동한다. |
 |
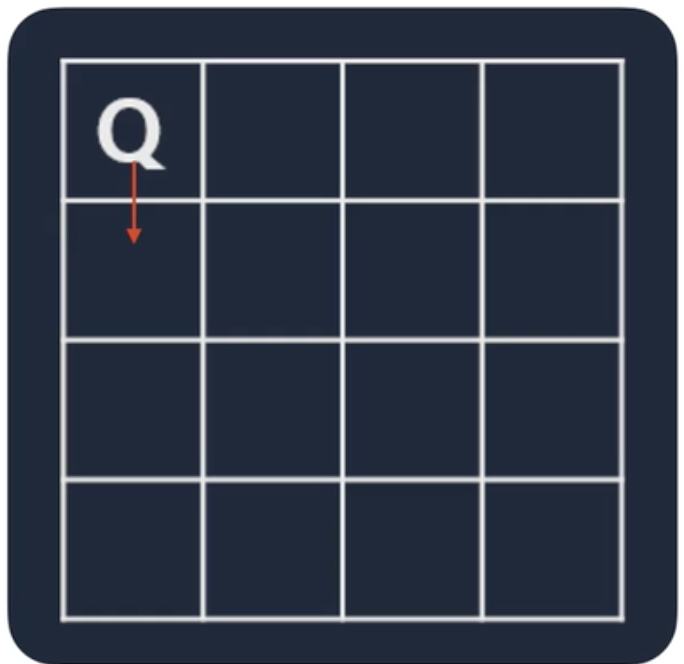
| 또 다른 가지치기를 할 수 있다. 두 번째 줄 첫 칸은 둘 수 없기에 패스한다. |
 |
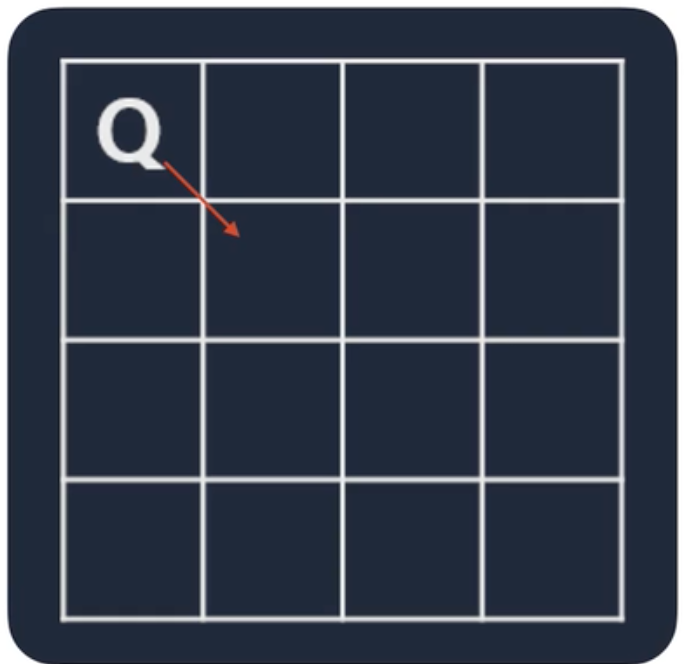
| 또 다른 가지치기를 할 수 있다. 마찬가지로 두 번째 줄 두 번째 칸은 둘 수 없기에 패스한다. |
 |
| 두 번째 줄 세 번째 칸은 퀸 배치가 가능하다. |  |
| 세 번째 줄에서 더 이상 퀸을 둘 수 없어서 이후 탐색은 제외한다. | 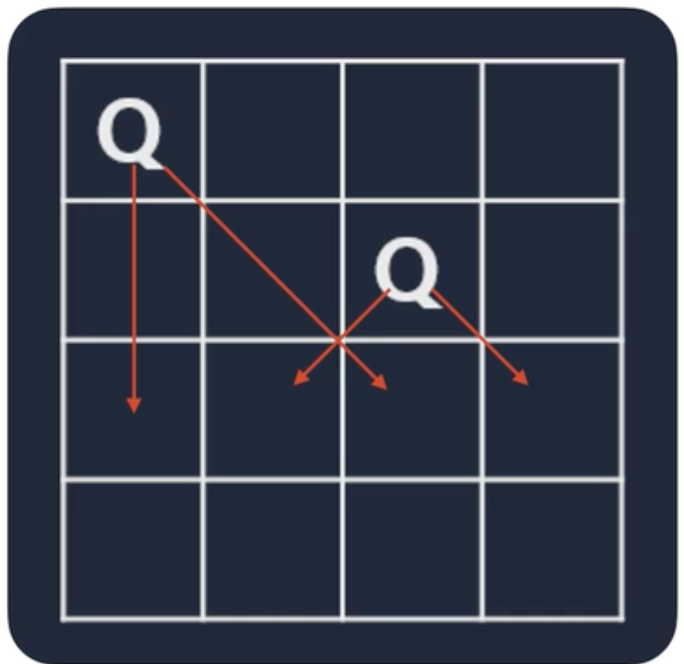 |
| 더이상 진행을 할 수 없으므로 다시 처음으로 돌아와서 이번엔 (1, 2)에 둬본다. |  |
| 안되는 곳은 패스하고 되는 곳에 둔다. |  |
| 세 번째 줄에서도 안되는 곳은 패스하고 되는 곳에 둔다. |  |
| 결과적으로 N개의 퀸을 배치할 수 있는 경우의 수를 찾았다. 이런식으로 백트래킹을 통해 모든 경우의 수를 찾을 수 있다. |
 |
✨ 관련 문제 풀이
https://lazyhysong.tistory.com/entry/JS-Backtracking-N-Queen
[JS] Backtracking - N-Queen
https://school.programmers.co.kr/learn/courses/30/lessons/12952 프로그래머스 코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는
lazyhysong.tistory.com
'알고리즘 > 이론' 카테고리의 다른 글
| [JS] 비트 마스크 (BitMask) (0) | 2023.08.03 |
|---|---|
| [JS] 동적 계획법 (Dynamic Programming) (0) | 2023.08.03 |
| [JS] 투포인터 (Two Pointer) (0) | 2023.08.01 |
| [JS] 최소 신장 트리 (MST) - Kruskal (0) | 2023.08.01 |
| [JS] 최단 경로 알고리즘 (Dijkstra) (0) | 2023.07.29 |
Comments




