Recent Posts
Recent Comments
게으른개발너D
[JS] 최단 경로 알고리즘 (Dijkstra) 본문

✨ 최단 경로 알고리즘
- 그래프에서 특정 정점에서 목적지까지 최단 경로를 구하는 알고리즘
- DFS, BFS도 최단 경로 알고리즘으로 사용할 수 있다.
- 대표적인 최단 경로 알고리즘
- BFS
- 다익스트라 (Dijkstra)
- 벨만-포드 (Bellman-Ford's)
- 플로이드 와샬 (Floyd Warchall)
- 목적에 따라 알고리즘을 선택할 수 있다.
BFS, DFS
그래프의 간선 가중치가 모두 같을 때 적합하다.

예를들어, 아래와 같이 2차원 배열(지도) 입력이 주어진 상태로 최단거리를 찾아야 한다면 BFS, DFS로 푸는 경우가 많다.

이 경우 배열의 한 칸이 정점이 된다.
그리고 위, 아래, 오른쪽, 왼쪽이 간선이 된다.
간선의 가중치는 공평하게 1이 된다.
만약 간선에 가중치가 있다면?
Dijkstra
그래프의 간선 가중치가 각각 다른 경우 적합하다.
간선에 각각 가중치가 있고 이 간선의 가중치가 각각 양수일 때 사용하기 적합한 알고리즘이다.

✨ 다익스트라 알고리즘
- Edsger Wybe Dijkstra가 고안한 최단 경로 알고리즘 (원래 발음은 데이크스트라에 가까움)
- 우선순위 큐를 이용하여 만들 수 있다.
- V가 정점의 수, E가 간선의 수일 때, 시간복잡도는 O(E log V)이다.
알고리즘 예시
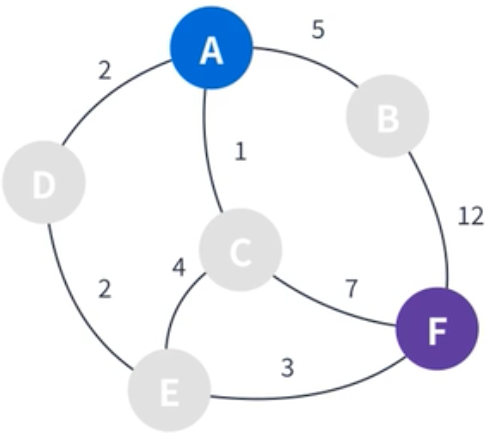
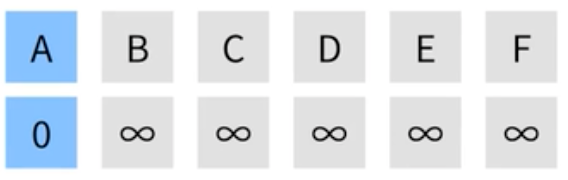
| 시작점을 제외한 나머지 정점의 거리는 모두 무한으로 초기화 한다. 여기서 시작점의 거리는 0으로 초기화 한다. |
 |
 |
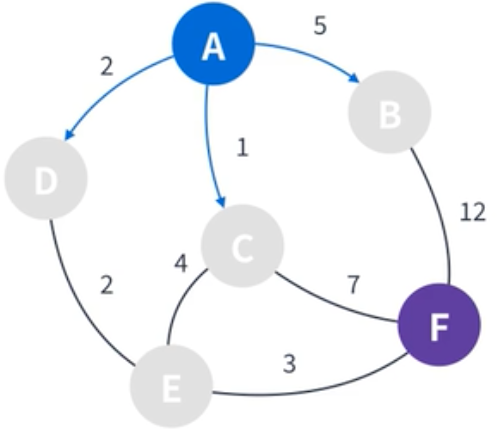
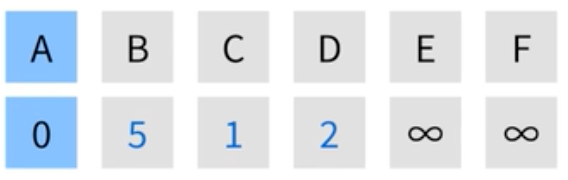
| 그 후 시작점에서 갈 수 있는 정점을 찾는다. 그리고나서 각 정점에 가중치를 더해준다. 여기서 B는 1이 되고, C는 1, D는 2가 된다. |
 |
 |
| 이어서, 설정한 정점 중 가장 최단거리가 짧은 정점을 선택한다. 여기서는 C가 1로 가장 작기에 C가 선택된다. |
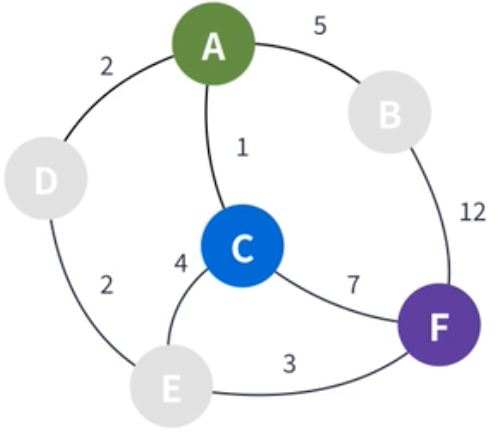 |
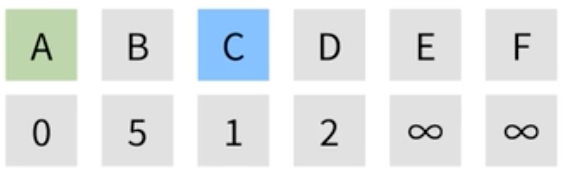 |
| C에서 갈 수 있는 정점을 찾고, 가중치를 더해준다. 갈 수 있는 정점은 E와 F가 있다. C까지의 거리인 1에서 각각 4과 7을 더해 E는 5가 되고 F는 8이 된다. |
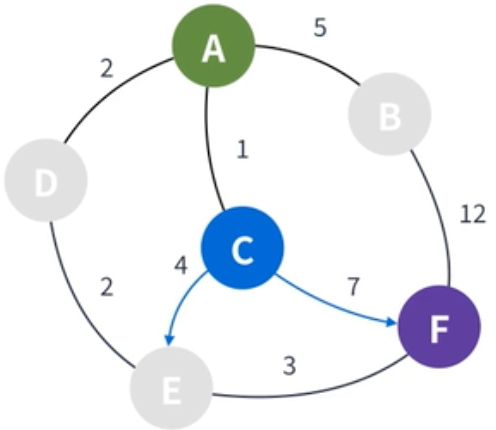 |
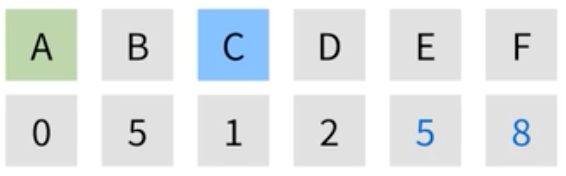 |
| C는 방문 처리하고, 다음으로 작은 정점인 D가 선택된다. | 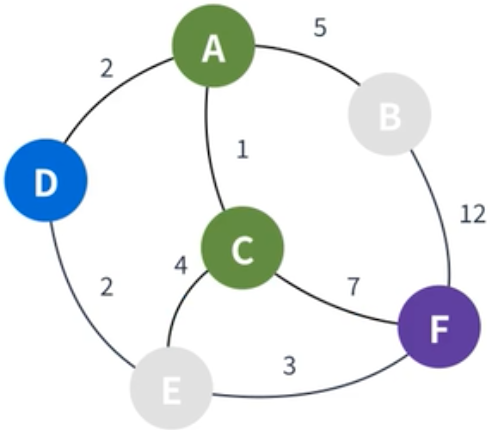 |
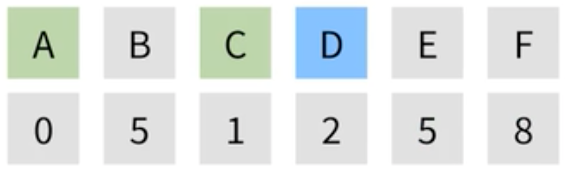 |
| D에서 갈 수 있는 정점은 E밖에 없다. E는 이미 값을 가지고 있지만 D에서 가는 가중치의 합이 더 작기 때문에 5에서 4로 갱신된다. |
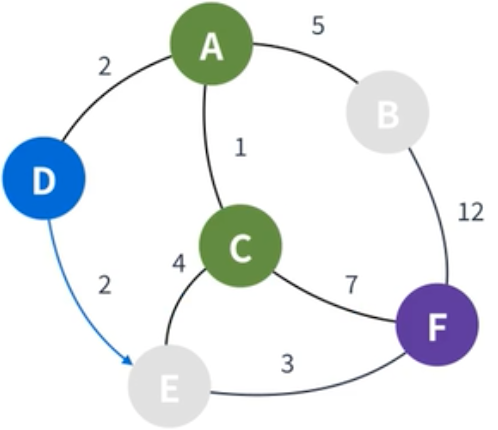 |
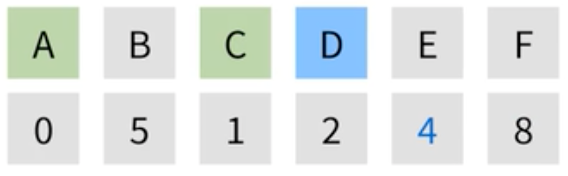 |
| D는 방문 처리하고, 다음으로 작은 정점인 E가 선택된다. | 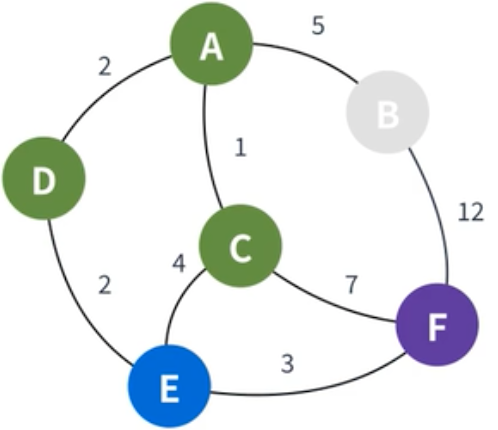 |
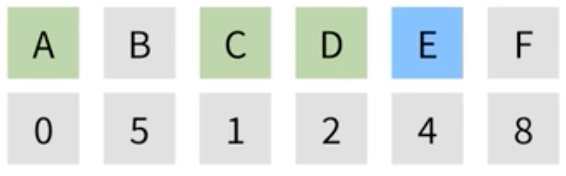 |
| E에서 갈 수 있는 정점은 F밖에 없기에, F로 가는 거리를 계산한다. 계산 결과, 가중치가 더 낮기때문에 기존 값은 8을 대체하여 7로 갱신한다. |
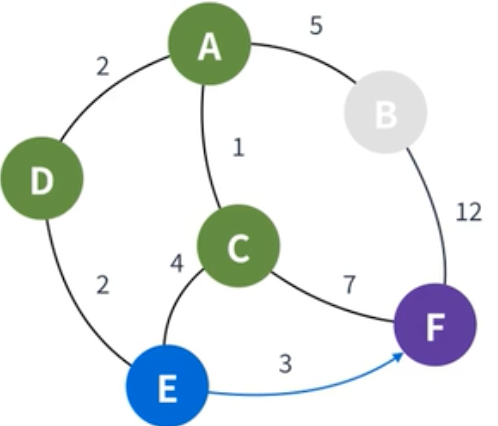 |
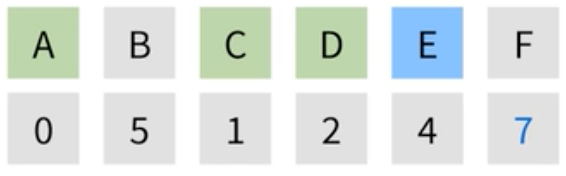 |
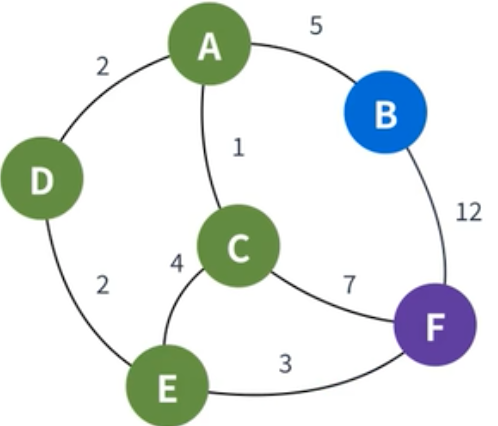
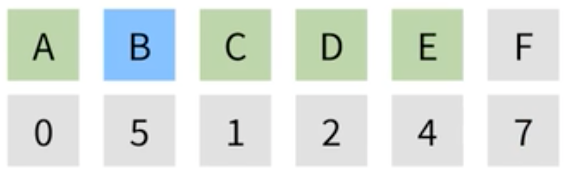
| E는 방문 처리하고, 도착점을 제외한 마지막 정점인 B를 선택해 준다. B에서 갈 수 있는 정점은 F밖에 없는데, 이번엔 계산한 가중치가 F의 값보다 크기 때문에 갱신하지 않는다. |
 |
 |
| 이제 결과적으로 도착점인 F만 남게 된다. | 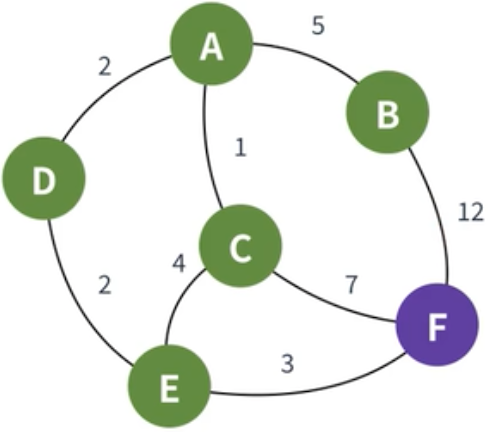 |
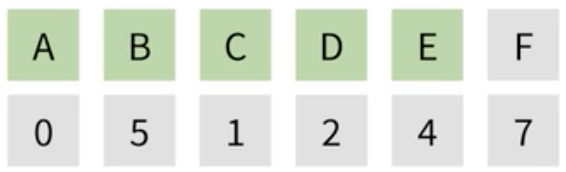 |
| F의 값을 확인해 보면, 가장 최단 경로인 7임을 알 수 있다. | 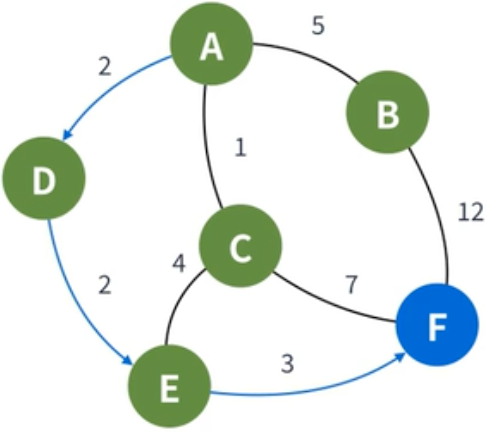 |
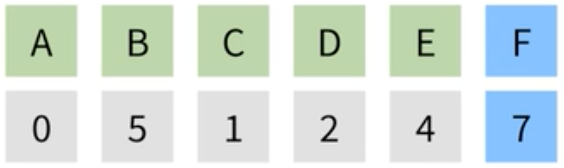 |
다익스트라 알고리즘의 핵심은 우선순위 큐!
가장 낮은 정점을 계속해서 선택해야한다.
따라서 이 부분이 우선순위 큐이고 이를 효율적으로 하기 위해 힙을 사용할 수가 있다.
알고리즘 정리
- 시작점을 제외한 모든 정점의 거리를 무한으로 설정한다. 시작점은 0으로 설정
- 시작점을 선택한다.
- 선택한 정점에서 갈 수 있는 정점의 거리를 정점(해당 정점까지의 최단 거리) 값 + 간선(거리) 값으로 갱신한다.
- 선택한 정점을 방문 처리한다.
- 이미 방문한 정점과 무한인 정점을 제외하고 가장 최단 거리인 정점을 선택한다.
- 더 이상 방문할 수 있는 정점이 없을 때까지 3~5를 반복한다.
- 도착점의 값을 확인한다.
✨ 관련 문제
https://lazyhysong.tistory.com/entry/JS-Dijkstra-%EB%B0%B0%EB%8B%AC
[JS] Dijkstra - 배달
https://school.programmers.co.kr/learn/courses/30/lessons/12978 프로그래머스 코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는
lazyhysong.tistory.com
'알고리즘 > 이론' 카테고리의 다른 글
| [JS] 투포인터 (Two Pointer) (0) | 2023.08.01 |
|---|---|
| [JS] 최소 신장 트리 (MST) - Kruskal (0) | 2023.08.01 |
| [JS] 재귀 함수 3 - 순열, 조합 (0) | 2023.07.18 |
| [JS] 재귀 함수 2 - 트리 순회 (0) | 2023.07.18 |
| [JS] 재귀 함수 1 (0) | 2023.07.18 |
Comments




